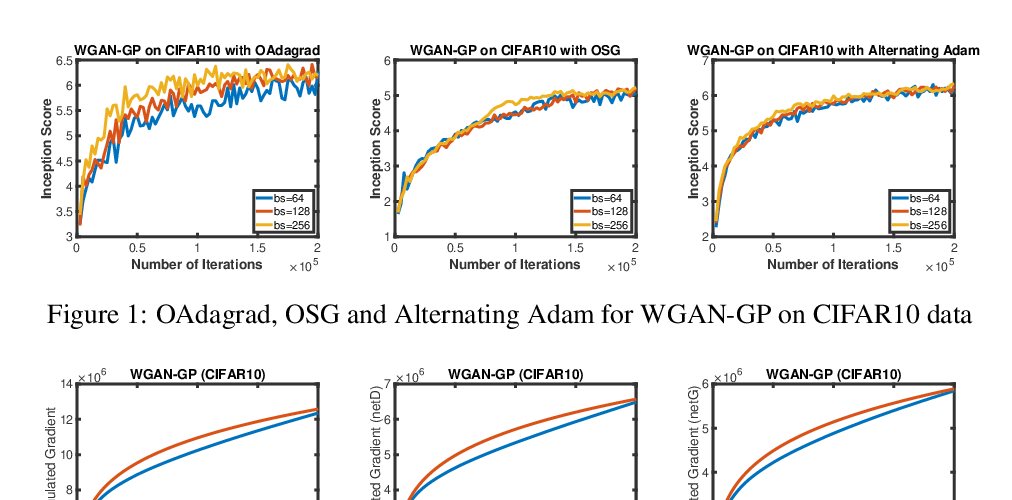
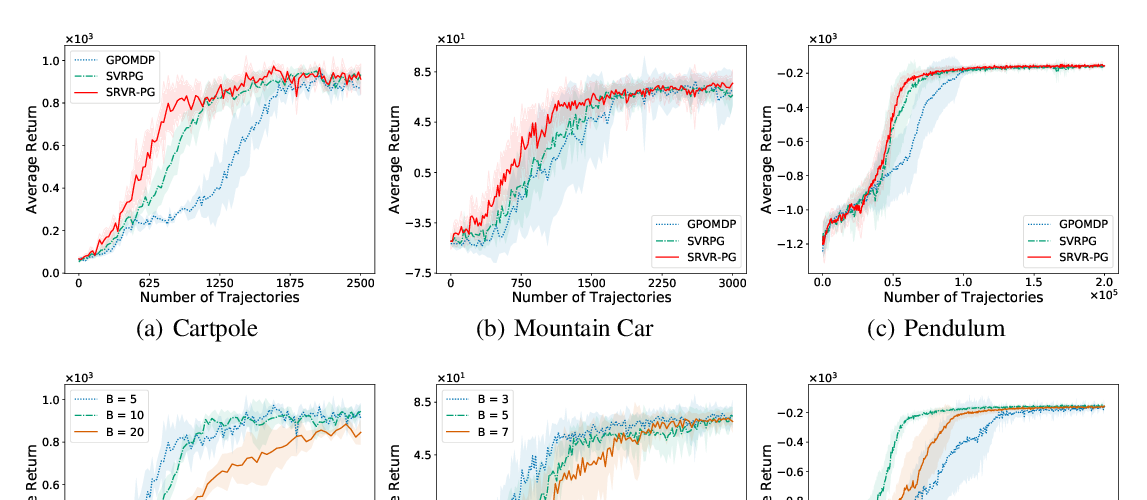
Abstract: Unseen data, which are not samples from the distribution of training data and are difficult to collect, have exhibited importance in numerous applications, ({\em e.g.,} novelty detection, semi-supervised learning, and adversarial training). In this paper, we introduce a general framework called \textbf{d}ifference-\textbf{s}eeking \textbf{g}enerative \textbf{a}dversarial \textbf{n}etwork (DSGAN), to generate various types of unseen data. Its novelty is the consideration of the probability density of the unseen data distribution as the difference between two distributions $p_{\bar{d}}$ and $p_{d}$ whose samples are relatively easy to collect. The DSGAN can learn the target distribution, $p_{t}$, (or the unseen data distribution) from only the samples from the two distributions, $p_{d}$ and $p_{\bar{d}}$. In our scenario, $p_d$ is the distribution of the seen data, and $p_{\bar{d}}$ can be obtained from $p_{d}$ via simple operations, so that we only need the samples of $p_{d}$ during the training. Two key applications, semi-supervised learning and novelty detection, are taken as case studies to illustrate that the DSGAN enables the production of various unseen data. We also provide theoretical analyses about the convergence of the DSGAN.