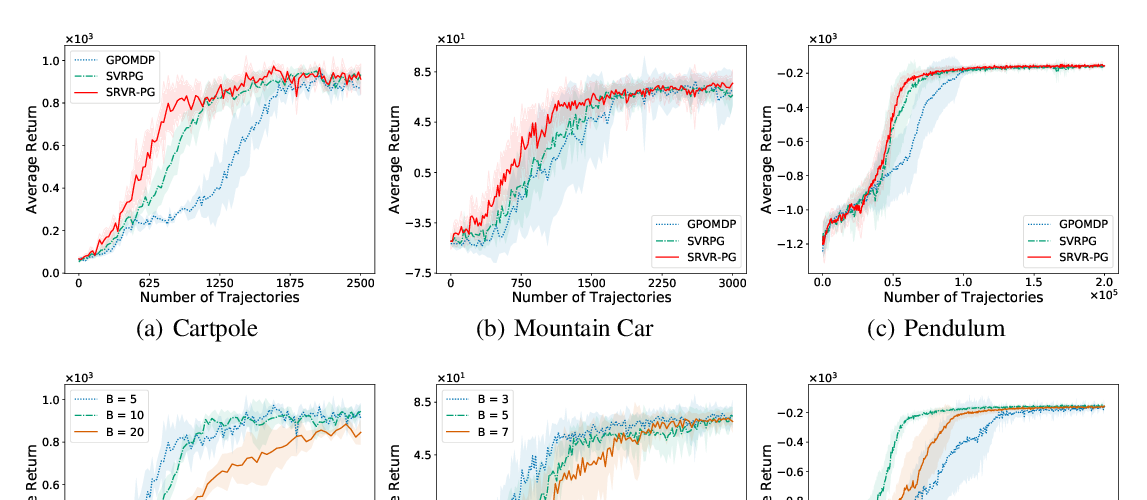
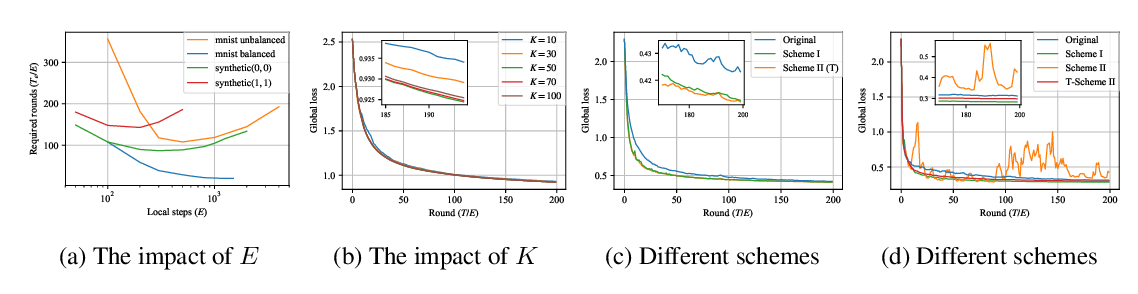
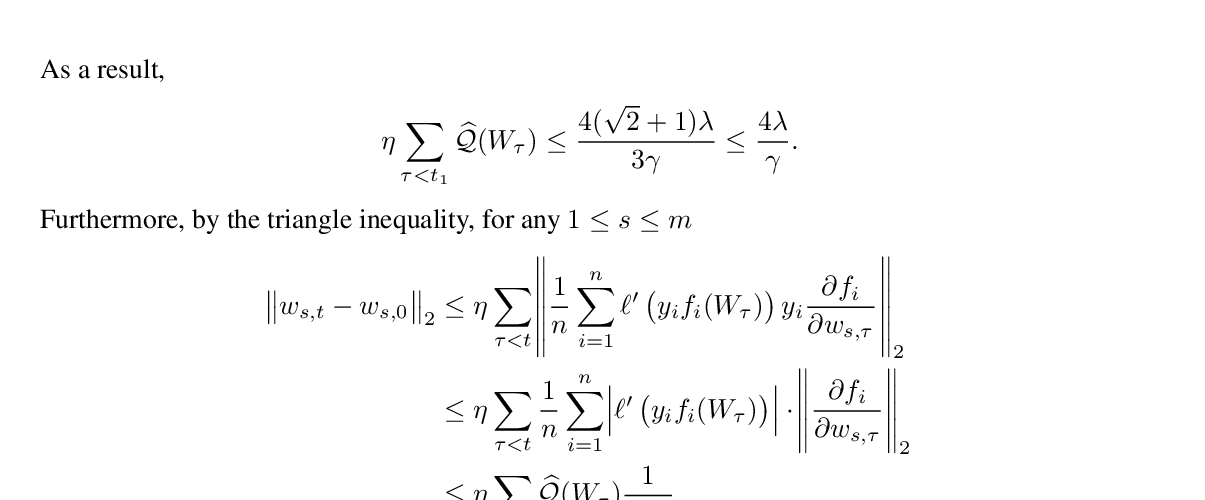Abstract:
Adaptive gradient algorithms perform gradient-based updates using the history of gradients and are ubiquitous in training deep neural networks. While adaptive gradient methods theory is well understood for minimization problems, the underlying factors driving their empirical success in min-max problems such as GANs remain unclear. In this paper, we aim at bridging this gap from both theoretical and empirical perspectives. First, we analyze a variant of Optimistic Stochastic Gradient (OSG) proposed in~\citep{daskalakis2017training} for solving a class of non-convex non-concave min-max problem and establish $O(\epsilon^{-4})$ complexity for finding $\epsilon$-first-order stationary point, in which the algorithm only requires invoking one stochastic first-order oracle while enjoying state-of-the-art iteration complexity achieved by stochastic extragradient method by~\citep{iusem2017extragradient}. Then we propose an adaptive variant of OSG named Optimistic Adagrad (OAdagrad) and reveal an \emph{improved} adaptive complexity $\widetilde{O}\left(\epsilon^{-\frac{2}{1-\alpha}}\right)$~\footnote{Here $\widetilde{O}(\cdot)$ compresses a logarithmic factor of $\epsilon$.}, where $\alpha$ characterizes the growth rate of the cumulative stochastic gradient and $0\leq \alpha\leq 1/2$. To the best of our knowledge, this is the first work for establishing adaptive complexity in non-convex non-concave min-max optimization. Empirically, our experiments show that indeed adaptive gradient algorithms outperform their non-adaptive counterparts in GAN training. Moreover, this observation can be explained by the slow growth rate of the cumulative stochastic gradient, as observed empirically.