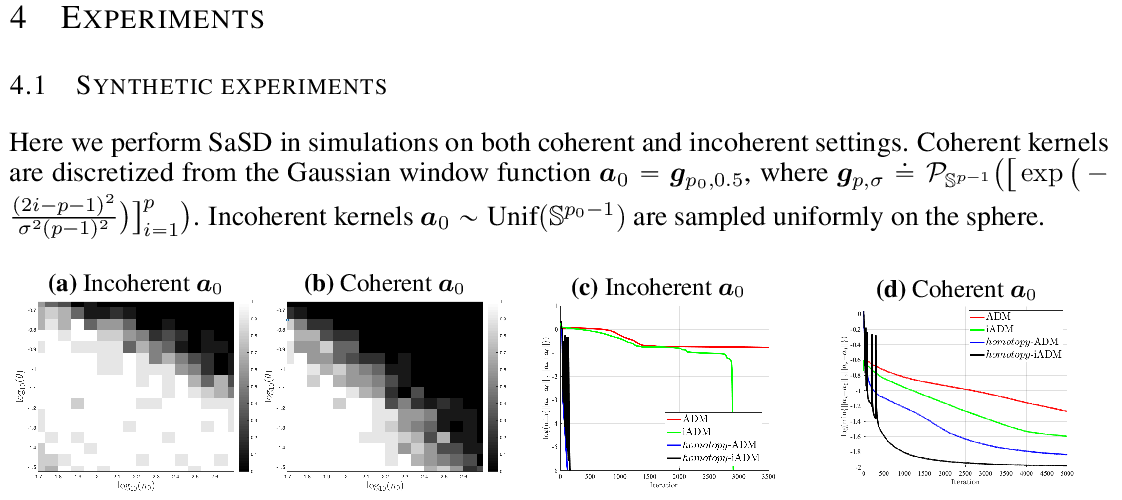
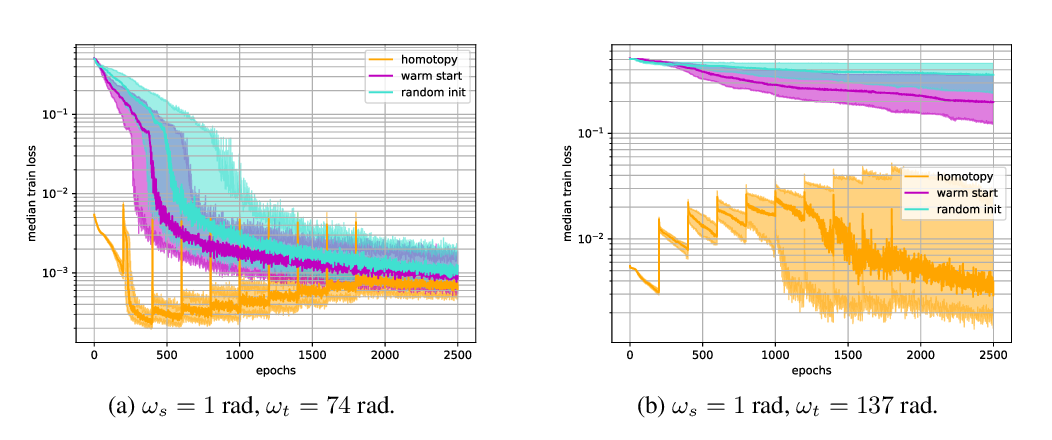
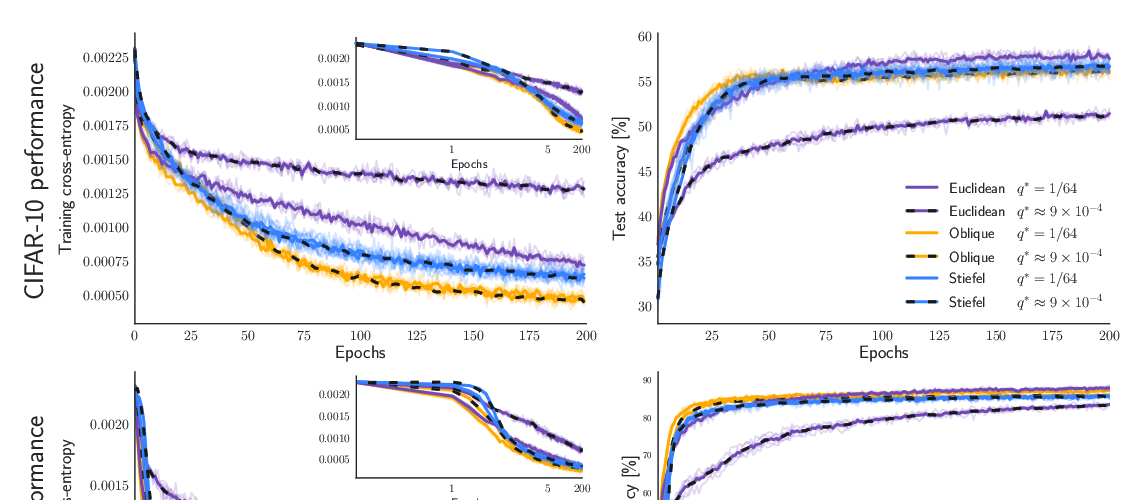
Abstract:
Learning overcomplete representations finds many applications in machine learning and data analytics. In the past decade, despite the empirical success of heuristic methods, theoretical understandings and explanations of these algorithms are still far from satisfactory. In this work, we provide new theoretical insights for several important representation learning problems: learning (i) sparsely used overcomplete dictionaries and (ii) convolutional dictionaries. We formulate these problems as $\ell^4$-norm optimization problems over the sphere and study the geometric properties of their nonconvex optimization landscapes. For both problems, we show the nonconvex objective has benign (global) geometric structures, which enable the development of efficient optimization methods finding the target solutions. Finally, our theoretical results are justified by numerical simulations.