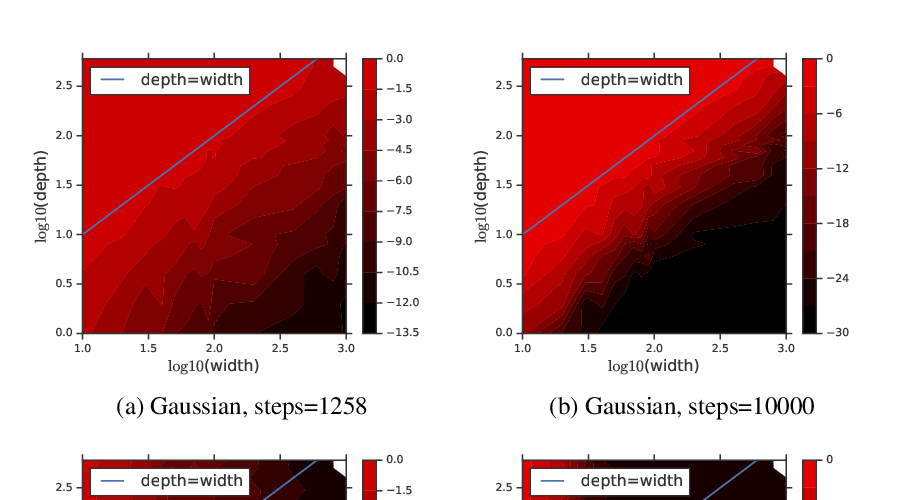
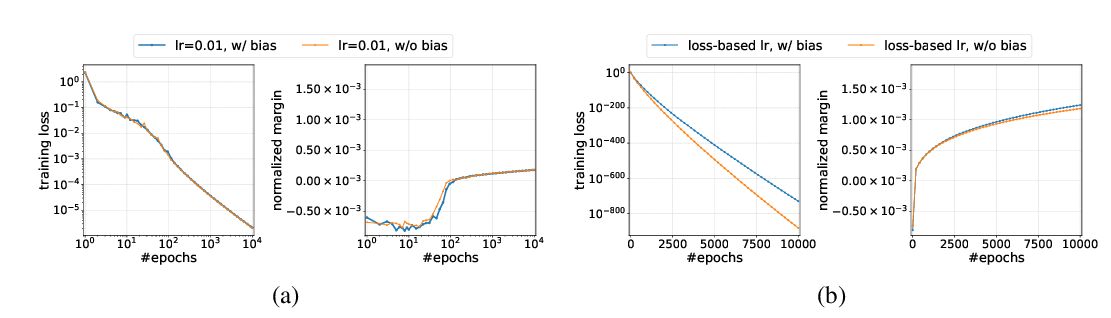
Abstract: Recently mean field theory has been successfully used to analyze properties of wide, random neural networks. It gave rise to a prescriptive theory for initializing feed-forward neural networks with orthogonal weights, which ensures that both the forward propagated activations and the backpropagated gradients are near \(\ell_2\) isometries and as a consequence training is orders of magnitude faster. Despite strong empirical performance, the mechanisms by which critical initializations confer an advantage in the optimization of deep neural networks are poorly understood. Here we show a novel connection between the maximum curvature of the optimization landscape (gradient smoothness) as measured by the Fisher information matrix (FIM) and the spectral radius of the input-output Jacobian, which partially explains why more isometric networks can train much faster. Furthermore, given that orthogonal weights are necessary to ensure that gradient norms are approximately preserved at initialization, we experimentally investigate the benefits of maintaining orthogonality throughout training, and we conclude that manifold optimization of weights performs well regardless of the smoothness of the gradients. Moreover, we observe a surprising yet robust behavior of highly isometric initializations --- even though such networks have a lower FIM condition number \emph{at initialization}, and therefore by analogy to convex functions should be easier to optimize, experimentally they prove to be much harder to train with stochastic gradient descent. We conjecture the FIM condition number plays a non-trivial role in the optimization.