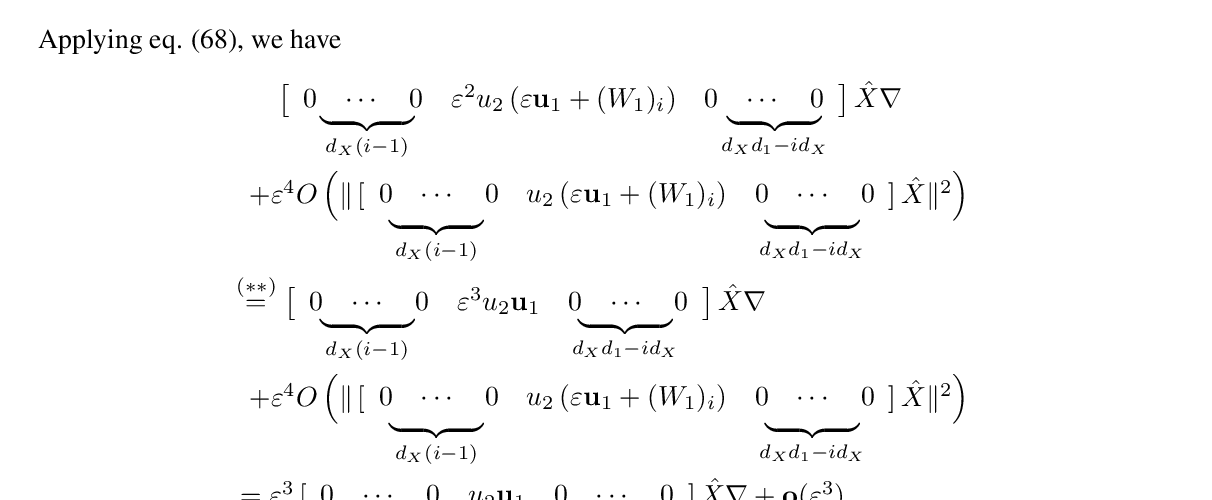Abstract: The critical locus of the loss function of a neural network is determined by the geometry of the functional space and by the parameterization of this space by the network's weights. We introduce a natural distinction between pure critical points, which only depend on the functional space, and spurious critical points, which arise from the parameterization. We apply this perspective to revisit and extend the literature on the loss function of linear neural networks. For this type of network, the functional space is either the set of all linear maps from input to output space, or a determinantal variety, i.e., a set of linear maps with bounded rank. We use geometric properties of determinantal varieties to derive new results on the landscape of linear networks with different loss functions and different parameterizations. Our analysis clearly illustrates that the absence of "bad" local minima in the loss landscape of linear networks is due to two distinct phenomena that apply in different settings: it is true for arbitrary smooth convex losses in the case of architectures that can express all linear maps ("filling architectures") but it holds only for the quadratic loss when the functional space is a determinantal variety ("non-filling architectures"). Without any assumption on the architecture, smooth convex losses may lead to landscapes with many bad minima.