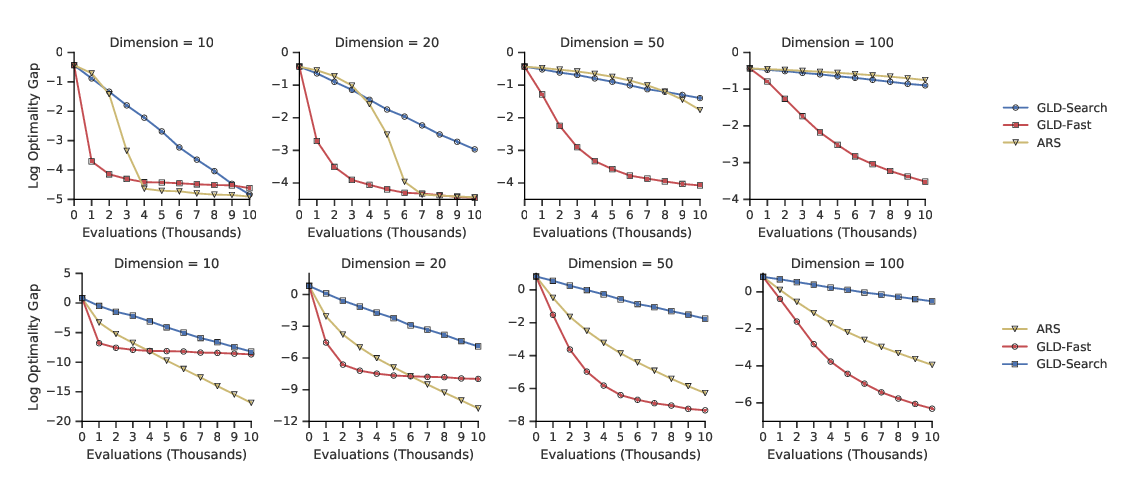
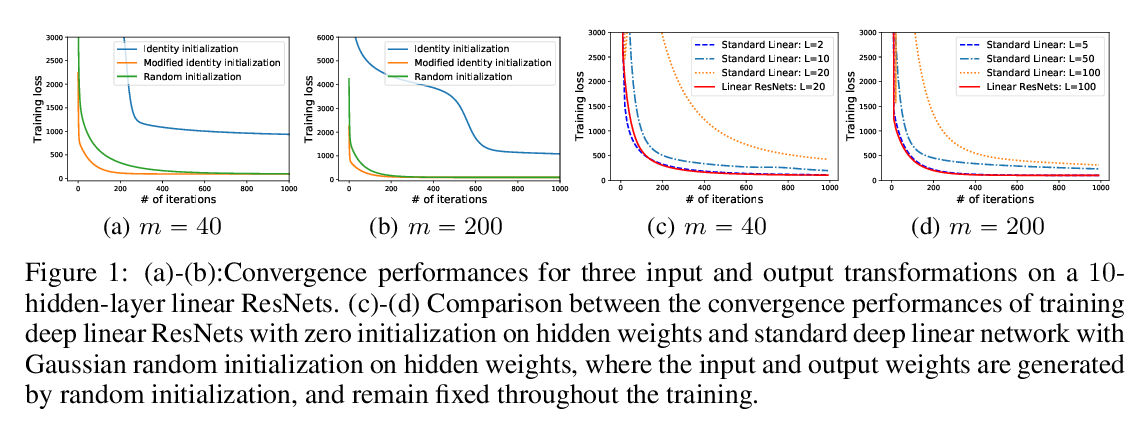
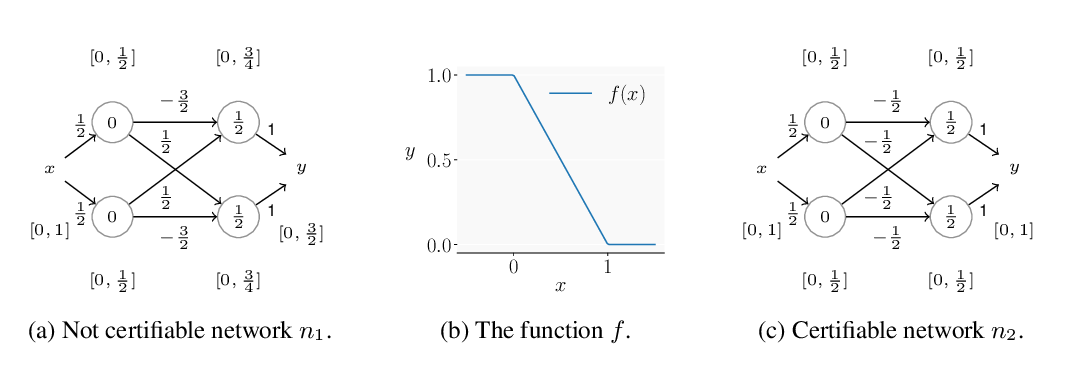
Abstract:
We study the landscape of squared loss in neural networks with one-hidden layer and ReLU activation functions. Let $m$ and $d$ be the widths of hidden and input layers, respectively. We show that there exist poor local minima with positive curvature for some training sets of size $n\geq m+2d-2$. By positive curvature of a local minimum, we mean that within a small neighborhood the loss function is strictly increasing in all directions. Consequently, for such training sets, there are initialization of weights from which there is no descent path to global optima. It is known that for $n\le m$, there always exist descent paths to global optima from all initial weights. In this perspective, our results provide a somewhat sharp characterization of the over-parameterization required for "existence of descent paths" in the loss landscape.