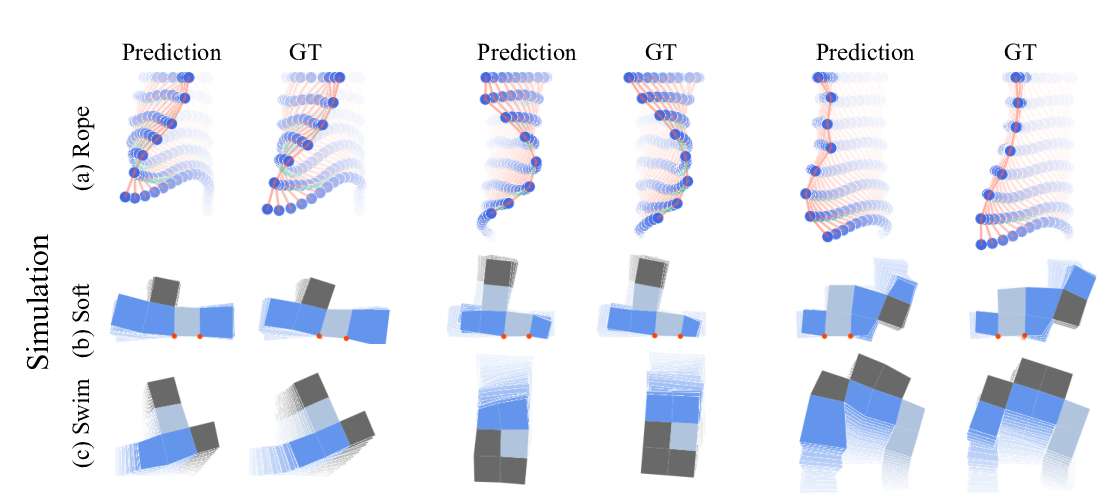
Abstract: We present a new approach to 3D object representation where a neural network encodes the geometry of an object directly into the weights and biases of a second 'mapping' network. This mapping network can be used to reconstruct an object by applying its encoded transformation to points randomly sampled from a simple geometric space, such as the unit sphere. We study the effectiveness of our method through various experiments on subsets of the ShapeNet dataset. We find that the proposed approach can reconstruct encoded objects with accuracy equal to or exceeding state-of-the-art methods with orders of magnitude fewer parameters. Our smallest mapping network has only about 7000 parameters and shows reconstruction quality on par with state-of-the-art object decoder architectures with millions of parameters. Further experiments on feature mixing through the composition of learned functions show that the encoding captures a meaningful subspace of objects.