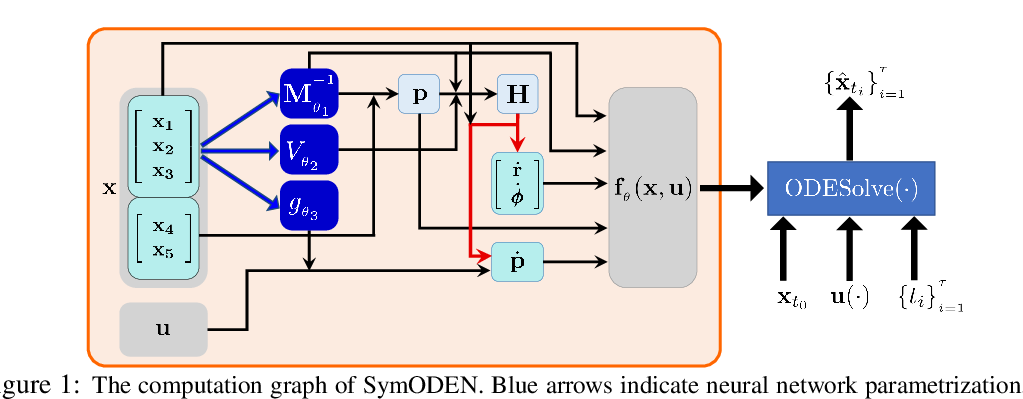
Abstract:
This paper presents a novel physics-inspired deep learning approach for point cloud processing motivated by the natural flow phenomena in fluid mechanics. Our learning architecture jointly defines data in an Eulerian world space, using a static background grid, and a Lagrangian material space, using moving particles. By introducing this Eulerian-Lagrangian representation, we are able to naturally evolve and accumulate particle features using flow velocities generated from a generalized, high-dimensional force field. We demonstrate the efficacy of this system by solving various point cloud classification and segmentation problems with state-of-the-art performance. The entire geometric reservoir and data flow mimic the pipeline of the classic PIC/FLIP scheme in modeling natural flow, bridging the disciplines of geometric machine learning and physical simulation.