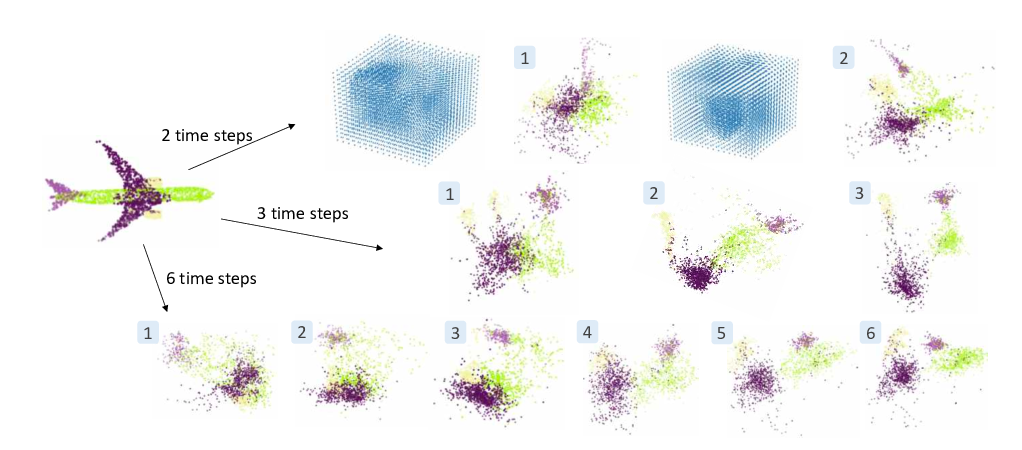
Abstract: We present an approach to Lagrangian fluid simulation with a new type of convolutional network. Our networks process sets of moving particles, which describe fluids in space and time. Unlike previous approaches, we do not build an explicit graph structure to connect the particles but use spatial convolutions as the main differentiable operation that relates particles to their neighbors. To this end we present a simple, novel, and effective extension of N-D convolutions to the continuous domain. We show that our network architecture can simulate different materials, generalizes to arbitrary collision geometries, and can be used for inverse problems. In addition, we demonstrate that our continuous convolutions outperform prior formulations in terms of accuracy and speed.