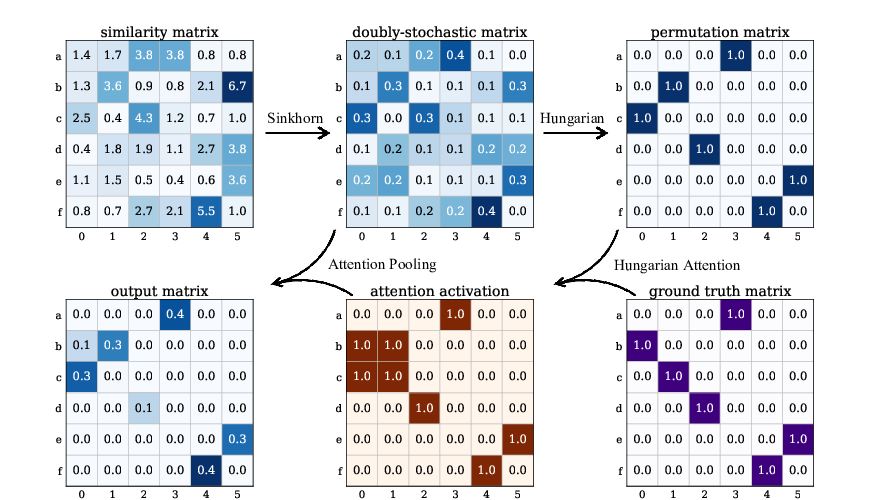
Abstract:
Achieving fusion of deep learning with combinatorial algorithms promises transformative changes to artificial intelligence. One possible approach is to introduce combinatorial building blocks into neural networks. Such end-to-end architectures have the potential to tackle combinatorial problems on raw input data such as ensuring global consistency in multi-object tracking or route planning on maps in robotics. In this work, we present a method that implements an efficient backward pass through blackbox implementations of combinatorial solvers with linear objective functions. We provide both theoretical and experimental backing. In particular, we incorporate the Gurobi MIP solver, Blossom V algorithm, and Dijkstra's algorithm into architectures that extract suitable features from raw inputs for the traveling salesman problem, the min-cost perfect matching problem and the shortest path problem.