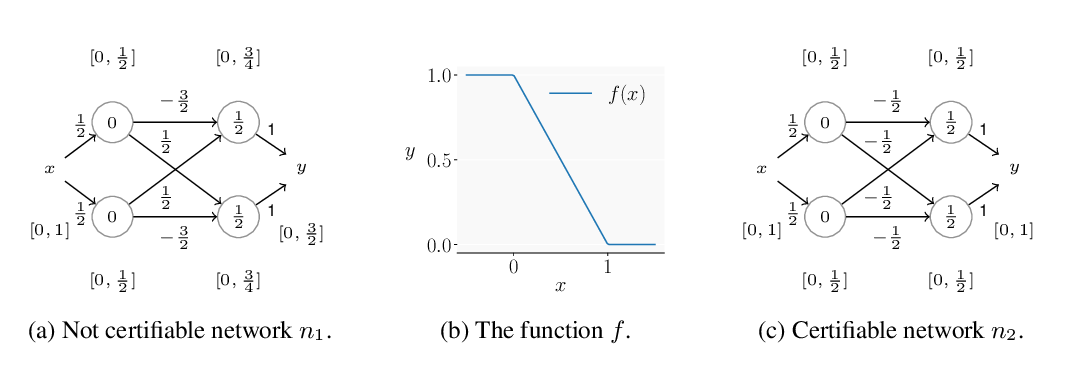
Abstract: We show how neural models can be used to realize piece-wise constant functions such as decision trees. Our approach builds on ReLU networks that are piece-wise linear and hence their associated gradients with respect to the inputs are locally constant. We formally establish the equivalence between the classes of locally constant networks and decision trees. Moreover, we highlight several advantageous properties of locally constant networks, including how they realize decision trees with parameter sharing across branching / leaves. Indeed, only $M$ neurons suffice to implicitly model an oblique decision tree with $2^M$ leaf nodes. The neural representation also enables us to adopt many tools developed for deep networks (e.g., DropConnect (Wan et al., 2013)) while implicitly training decision trees. We demonstrate that our method outperforms alternative techniques for training oblique decision trees in the context of molecular property classification and regression tasks.