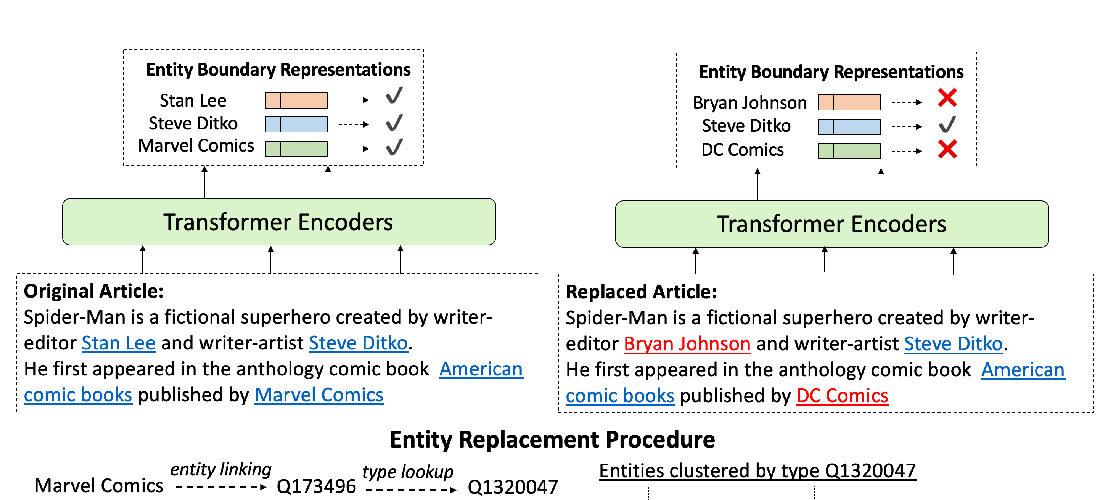
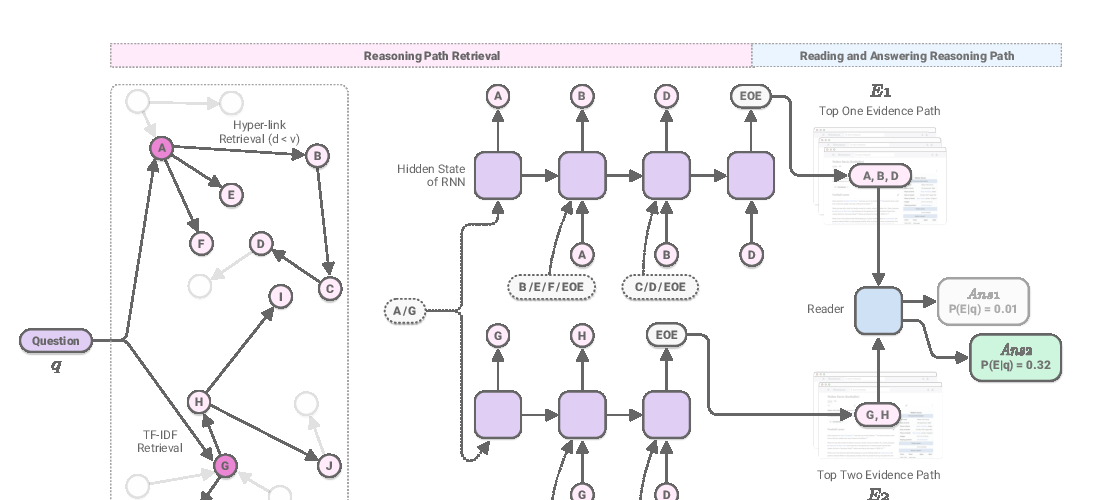
Abstract: Integrating distributed representations with symbolic operations is essential for reading comprehension requiring complex reasoning, such as counting, sorting and arithmetics, but most existing approaches are hard to scale to more domains or more complex reasoning. In this work, we propose the Neural Symbolic Reader (NeRd), which includes a reader, e.g., BERT, to encode the passage and question, and a programmer, e.g., LSTM, to generate a program that is executed to produce the answer. Compared to previous works, NeRd is more scalable in two aspects: (1) domain-agnostic, i.e., the same neural architecture works for different domains; (2) compositional, i.e., when needed, complex programs can be generated by recursively applying the predefined operators, which become executable and interpretable representations for more complex reasoning. Furthermore, to overcome the challenge of training NeRd with weak supervision, we apply data augmentation techniques and hard Expectation-Maximization (EM) with thresholding. On DROP, a challenging reading comprehension dataset that requires discrete reasoning, NeRd achieves 1.37%/1.18% absolute improvement over the state-of-the-art on EM/F1 metrics. With the same architecture, NeRd significantly outperforms the baselines on MathQA, a math problem benchmark that requires multiple steps of reasoning, by 25.5% absolute increment on accuracy when trained on all the annotated programs. More importantly, NeRd still beats the baselines even when only 20% of the program annotations are given.