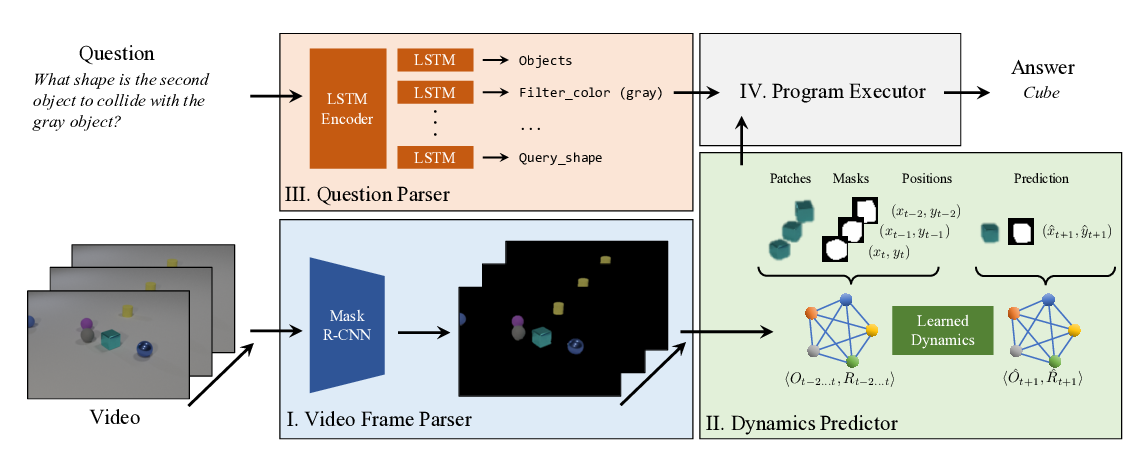
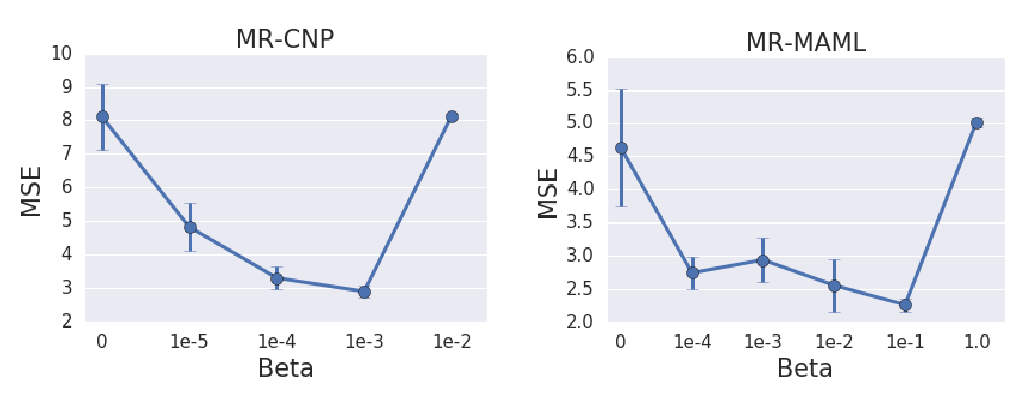
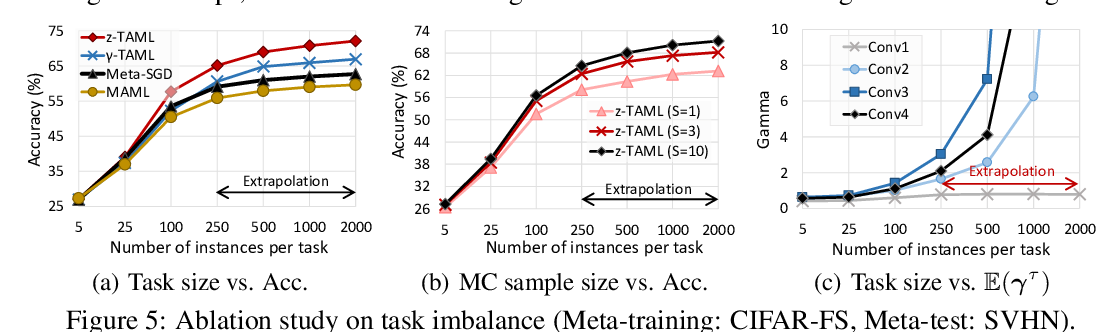
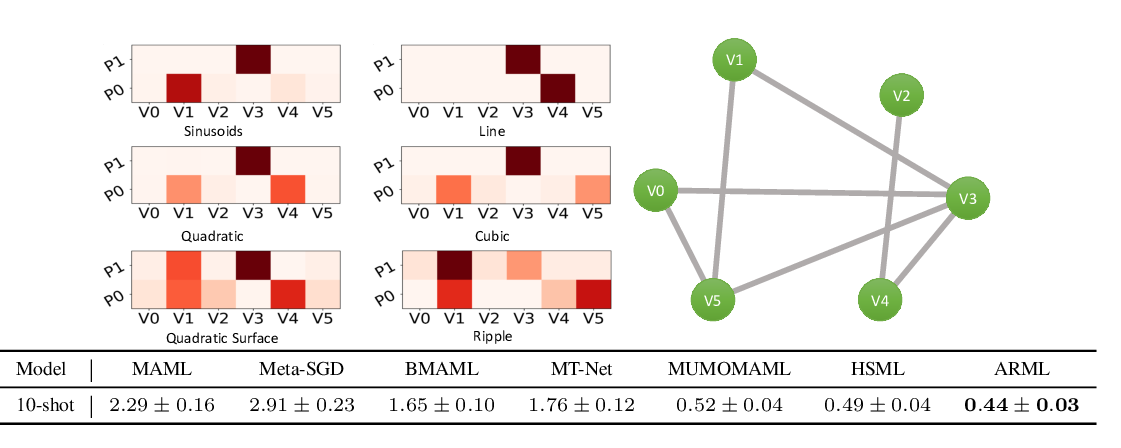
Abstract: We propose to use a meta-learning objective that maximizes the speed of transfer on a modified distribution to learn how to modularize acquired knowledge. In particular, we focus on how to factor a joint distribution into appropriate conditionals, consistent with the causal directions. We explain when this can work, using the assumption that the changes in distributions are localized (e.g. to one of the marginals, for example due to an intervention on one of the variables). We prove that under this assumption of localized changes in causal mechanisms, the correct causal graph will tend to have only a few of its parameters with non-zero gradient, i.e. that need to be adapted (those of the modified variables). We argue and observe experimentally that this leads to faster adaptation, and use this property to define a meta-learning surrogate score which, in addition to a continuous parametrization of graphs, would favour correct causal graphs. Finally, motivated by the AI agent point of view (e.g. of a robot discovering its environment autonomously), we consider how the same objective can discover the causal variables themselves, as a transformation of observed low-level variables with no causal meaning. Experiments in the two-variable case validate the proposed ideas and theoretical results.