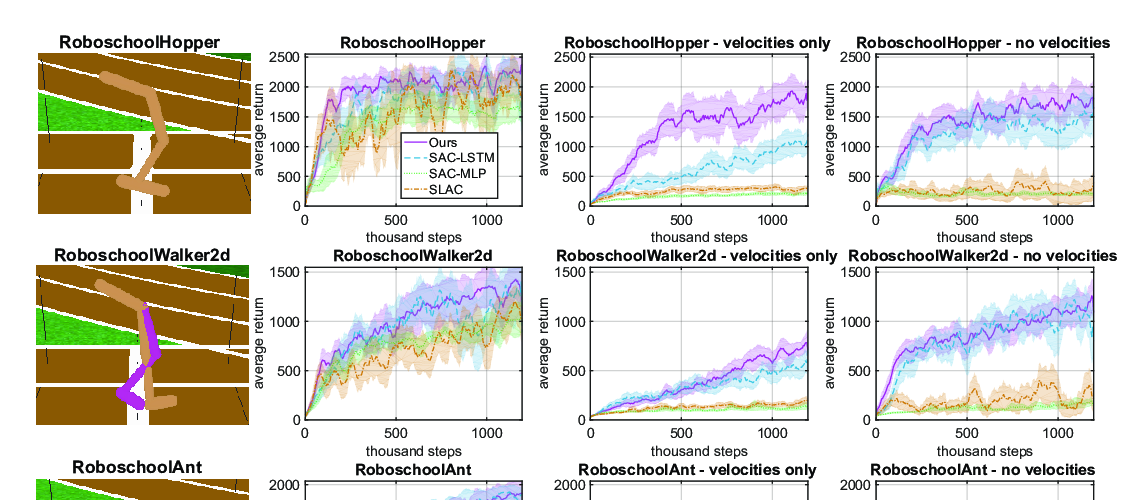
Abstract: Partially Observable Markov Decision Processes (POMDPs) are popular and flexible models for real-world decision-making applications that demand the information from past observations to make optimal decisions. Standard reinforcement learning algorithms for solving Markov Decision Processes (MDP) tasks are not applicable, as they cannot infer the unobserved states. In this paper, we propose a novel algorithm for POMDPs, named sequential variational soft Q-learning networks (SVQNs), which formalizes the inference of hidden states and maximum entropy reinforcement learning (MERL) under a unified graphical model and optimizes the two modules jointly. We further design a deep recurrent neural network to reduce the computational complexity of the algorithm. Experimental results show that SVQNs can utilize past information to help decision making for efficient inference, and outperforms other baselines on several challenging tasks. Our ablation study shows that SVQNs have the generalization ability over time and are robust to the disturbance of the observation.