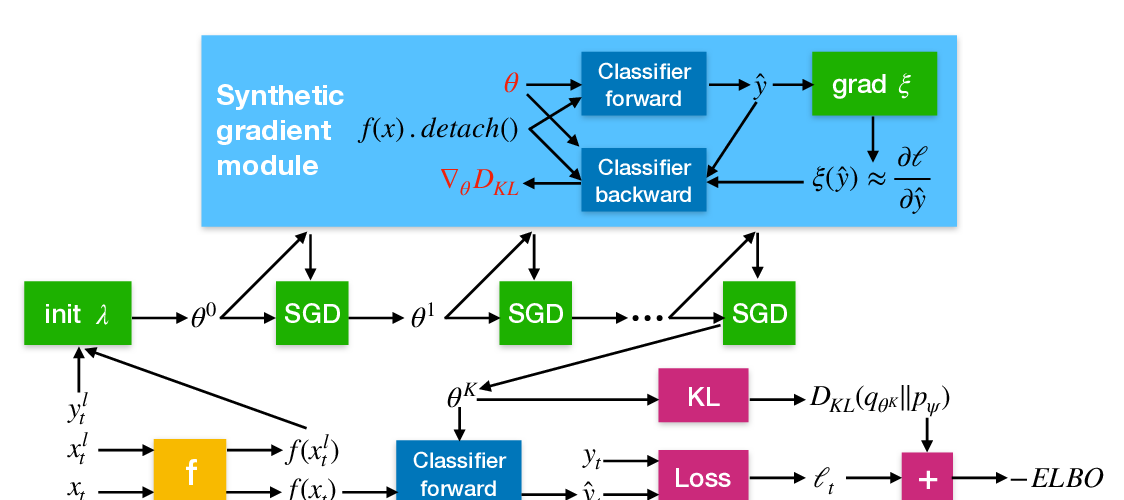
Abstract:
We propose a black-box algorithm called {\it Adversarial Variational Inference and Learning} (AdVIL) to perform inference and learning on a general Markov random field (MRF). AdVIL employs two variational distributions to approximately infer the latent variables and estimate the partition function of an MRF, respectively. The two variational distributions provide an estimate of the negative log-likelihood of the MRF as a minimax optimization problem, which is solved by stochastic gradient descent. AdVIL is proven convergent under certain conditions. On one hand, compared with contrastive divergence, AdVIL requires a minimal assumption about the model structure and can deal with a broader family of MRFs. On the other hand, compared with existing black-box methods, AdVIL provides a tighter estimate of the log partition function and achieves much better empirical results.