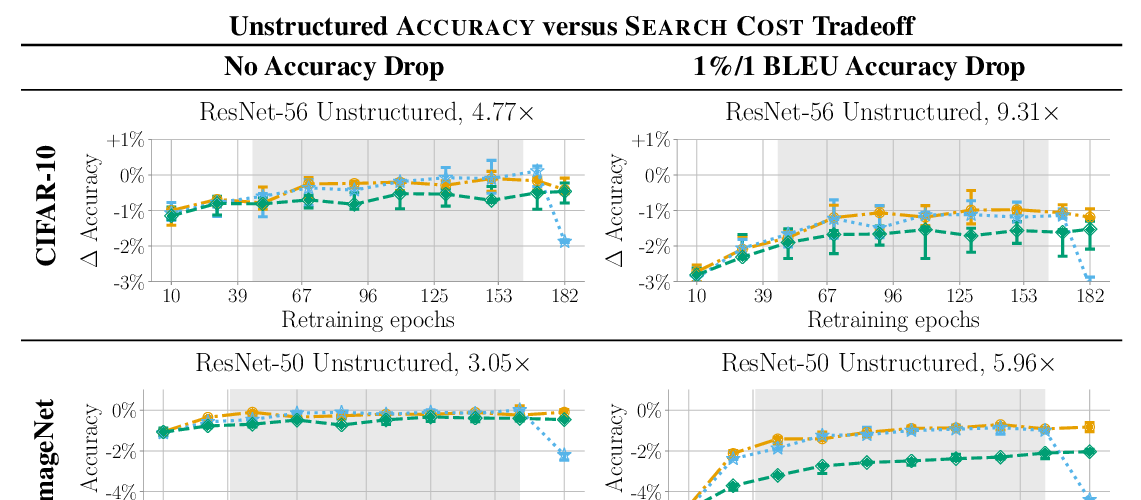
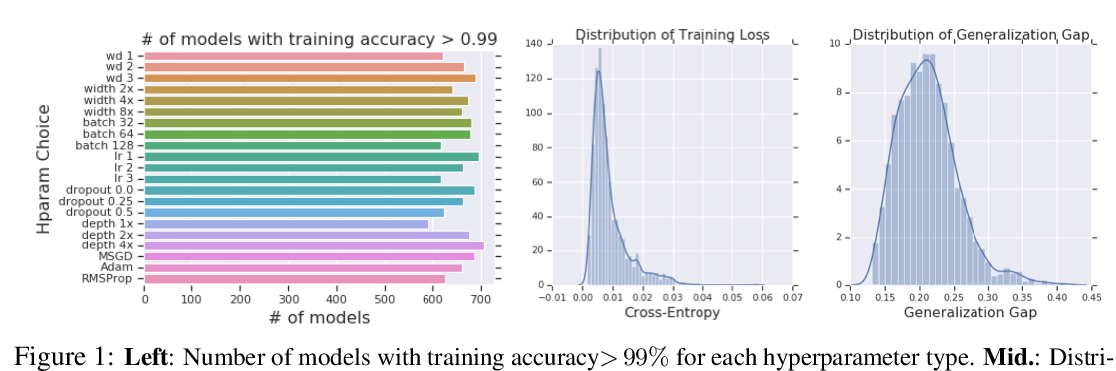
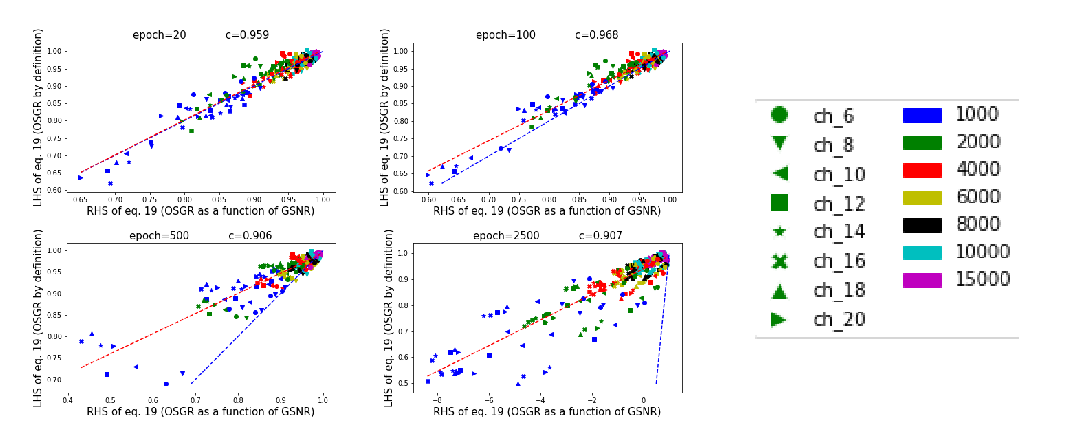
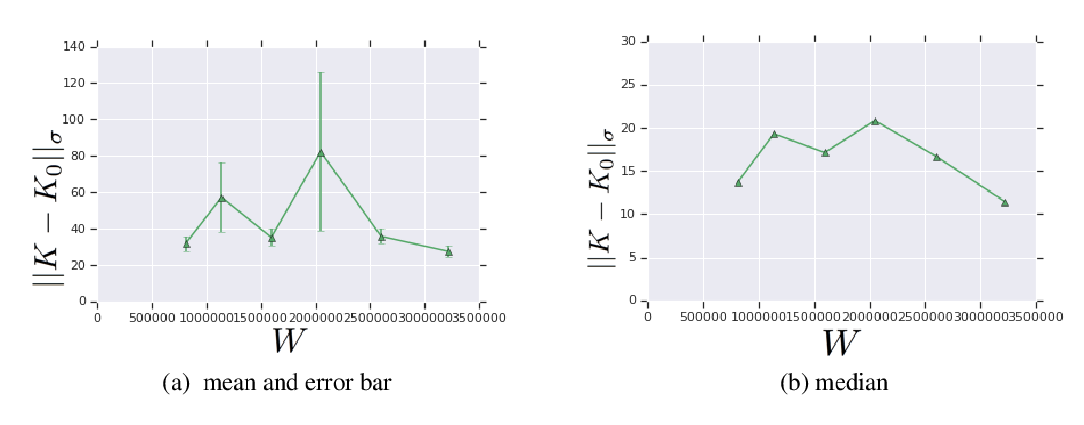
Abstract: We study the phenomenon that some modules of deep neural networks (DNNs) are more critical than others. Meaning that rewinding their parameter values back to initialization, while keeping other modules fixed at the trained parameters, results in a large drop in the network's performance. Our analysis reveals interesting properties of the loss landscape which leads us to propose a complexity measure, called module criticality, based on the shape of the valleys that connect the initial and final values of the module parameters. We formulate how generalization relates to the module criticality, and show that this measure is able to explain the superior generalization performance of some architectures over others, whereas, earlier measures fail to do so.