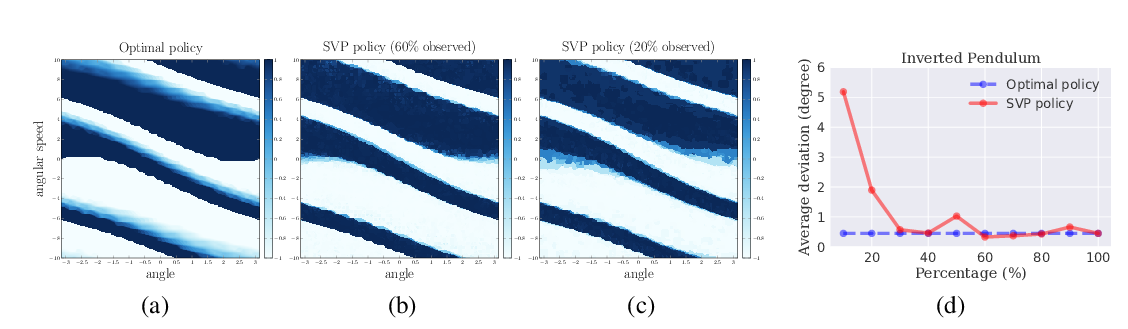
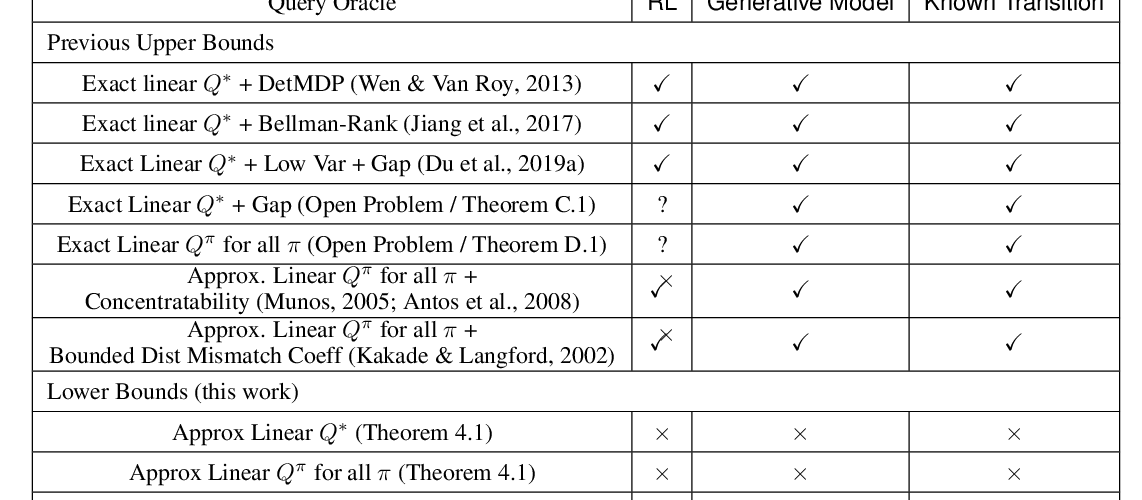
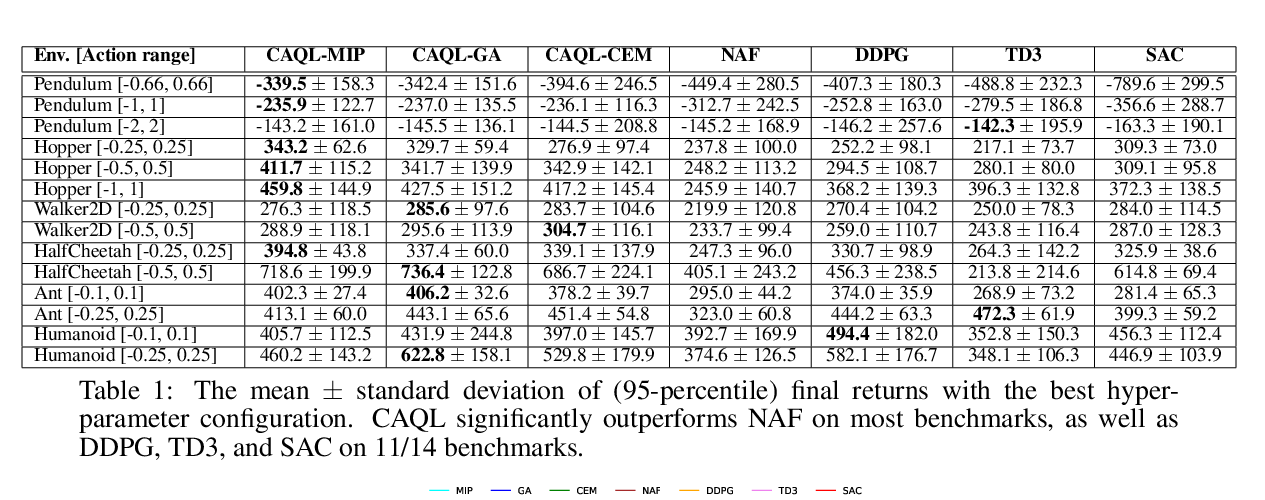
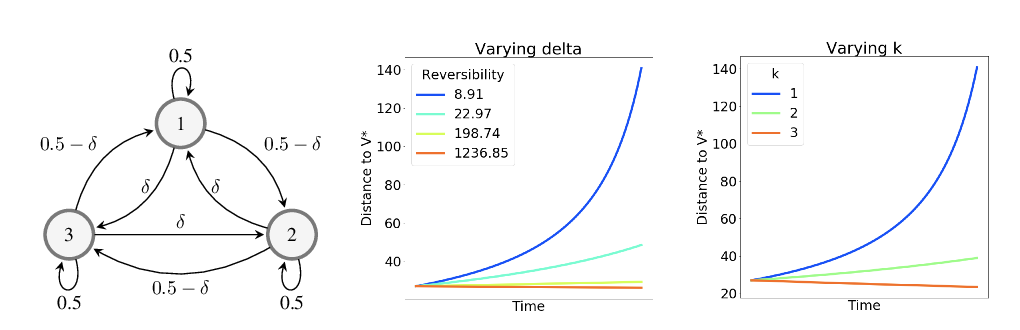
Abstract:
We analyze the Gambler's problem, a simple reinforcement learning problem where the gambler has the chance to double or lose their bets until the target is reached. This is an early example introduced in the reinforcement learning textbook by Sutton and Barto (2018), where they mention an interesting pattern of the optimal value function with high-frequency components and repeating non-smooth points. It is however without further investigation. We provide the exact formula for the optimal value function for both the discrete and the continuous cases. Though simple as it might seem, the value function is pathological: fractal, self-similar, derivative taking either zero or infinity, not smooth on any interval, and not written as elementary functions. It is in fact one of the generalized Cantor functions, where it holds a complexity that has been uncharted thus far. Our analyses could lead insights into improving value function approximation, gradient-based algorithms, and Q-learning, in real applications and implementations.