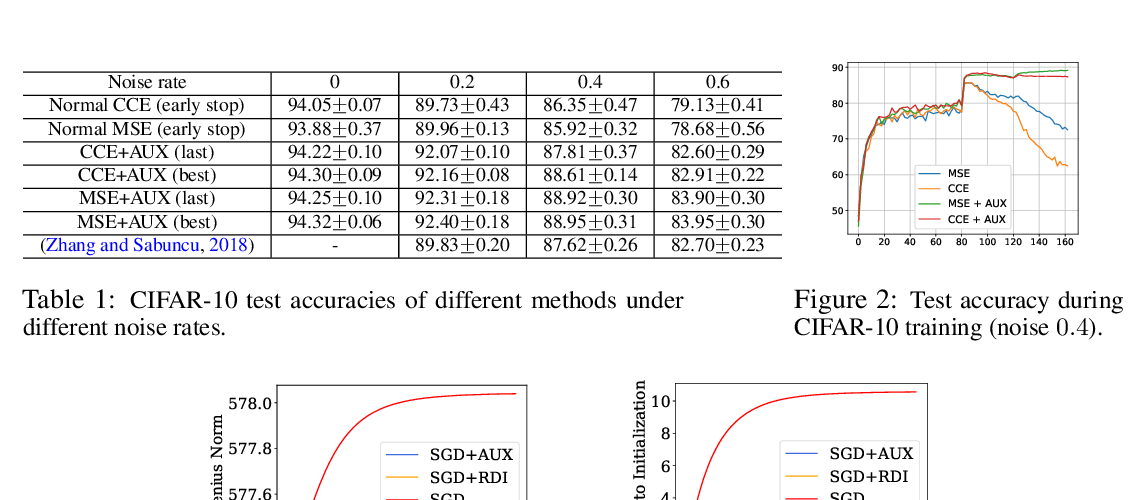
Abstract:
We study the generalization properties of deep convolutional neural networks for image denoising in the presence of varying noise levels. We provide extensive empirical evidence that current state-of-the-art architectures systematically overfit to the noise levels in the training set, performing very poorly at new noise levels. We show that strong generalization can be achieved through a simple architectural modification: removing all additive constants. The resulting "bias-free" networks attain state-of-the-art performance over a broad range of noise levels, even when trained over a limited range. They are also locally linear, which enables direct analysis with linear-algebraic tools. We show that the denoising map can be visualized locally as a filter that adapts to both image structure and noise level. In addition, our analysis reveals that deep networks implicitly perform a projection onto an adaptively-selected low-dimensional subspace, with dimensionality inversely proportional to noise level, that captures features of natural images.