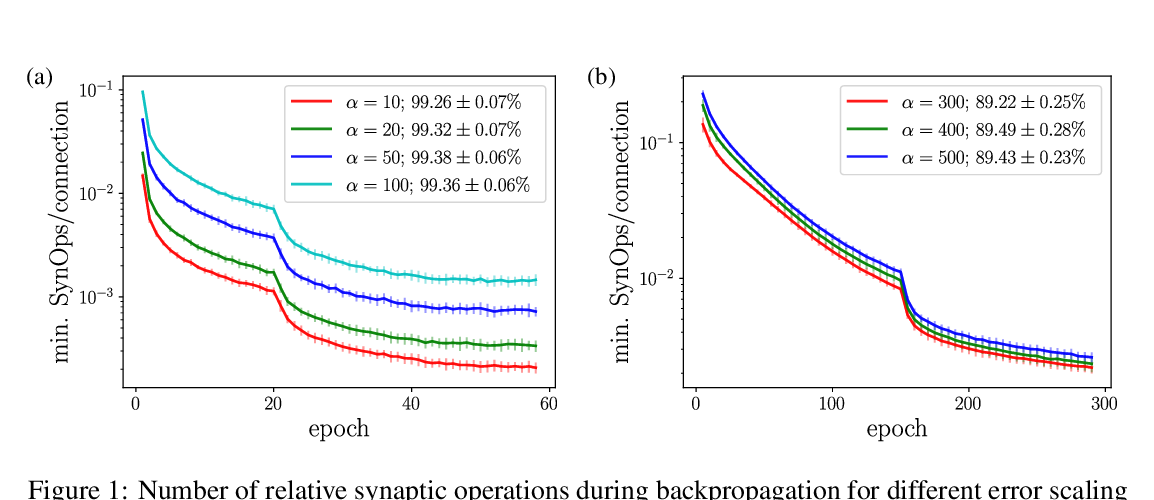
Abstract:
Neural networks can approximate complex functions, but they struggle to perform exact arithmetic operations over real numbers. The lack of inductive bias for arithmetic operations leaves neural networks without the underlying logic necessary to extrapolate on tasks such as addition, subtraction, and multiplication. We present two new neural network components: the Neural Addition Unit (NAU), which can learn exact addition and subtraction; and the Neural Multiplication Unit (NMU) that can multiply subsets of a vector. The NMU is, to our knowledge, the first arithmetic neural network component that can learn to multiply elements from a vector, when the hidden size is large. The two new components draw inspiration from a theoretical analysis of recently proposed arithmetic components. We find that careful initialization, restricting parameter space, and regularizing for sparsity is important when optimizing the NAU and NMU. Our proposed units NAU and NMU, compared with previous neural units, converge more consistently, have fewer parameters, learn faster, can converge for larger hidden sizes, obtain sparse and meaningful weights, and can extrapolate to negative and small values.