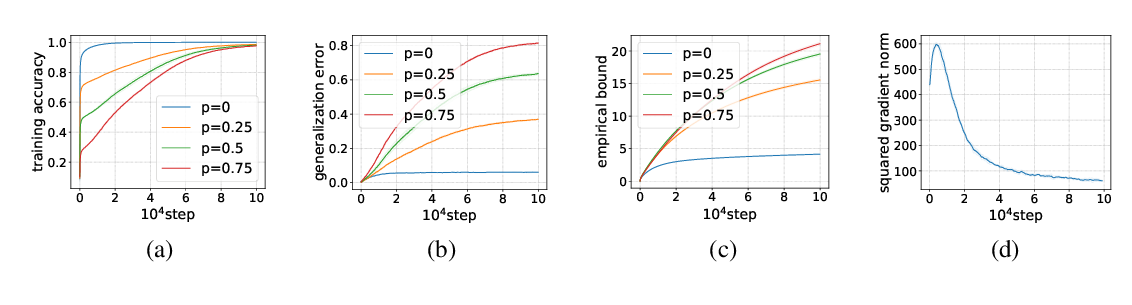
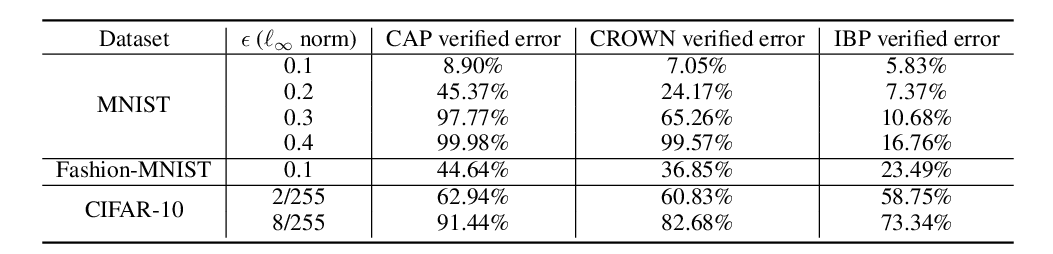
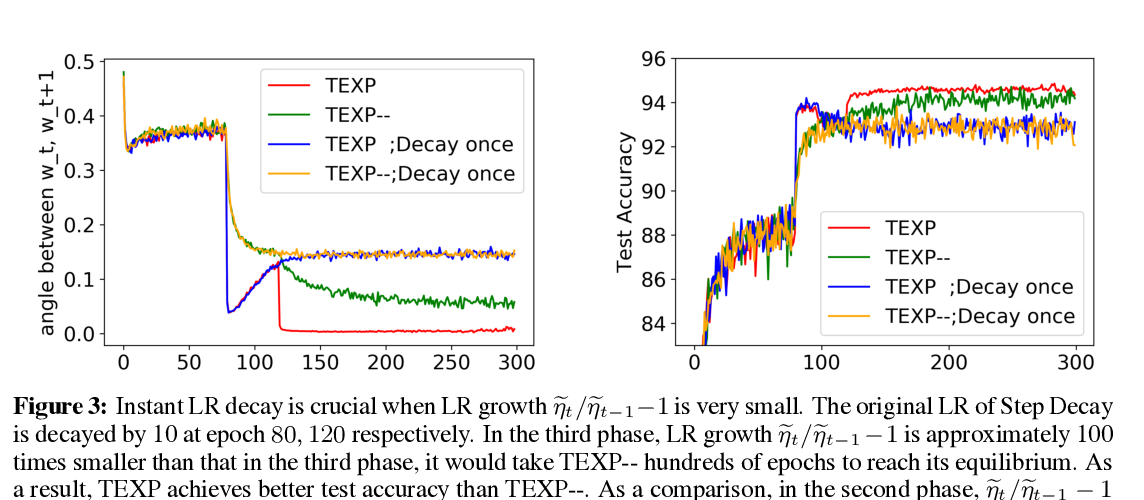
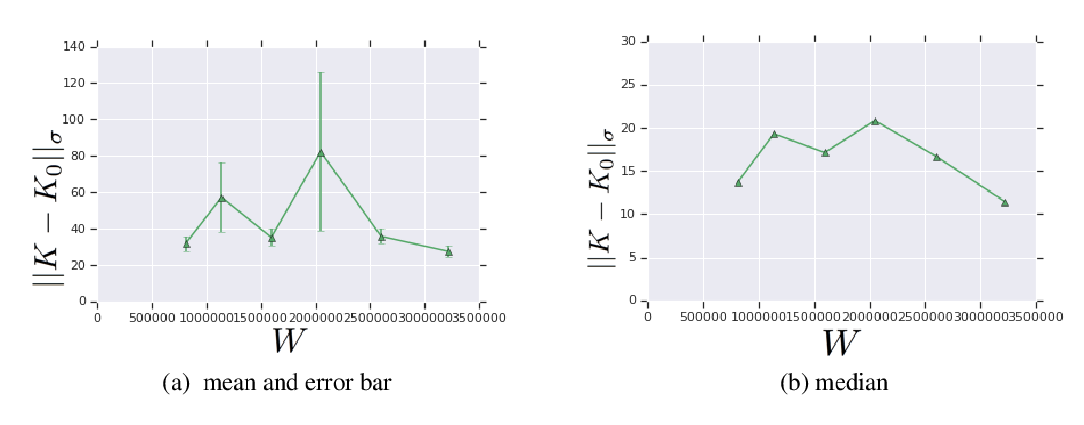
Abstract: Exciting new work on generalization bounds for neural networks (NN) given by Bartlett et al. (2017); Neyshabur et al. (2018) closely depend on two parameter- dependant quantities: the Lipschitz constant upper bound and the stable rank (a softer version of rank). Even though these bounds typically have minimal practical utility, they facilitate questions on whether controlling such quantities together could improve the generalization behaviour of NNs in practice. To this end, we propose stable rank normalization (SRN), a novel, provably optimal, and computationally efficient weight-normalization scheme which minimizes the stable rank of a linear operator. Surprisingly we find that SRN, despite being non-convex, can be shown to have a unique optimal solution. We provide extensive analyses across a wide variety of NNs (DenseNet, WideResNet, ResNet, Alexnet, VGG), where applying SRN to their linear layers leads to improved classification accuracy, while simultaneously showing improvements in genealization, evaluated empirically using—(a) shattering experiments (Zhang et al., 2016); and (b) three measures of sample complexity by Bartlett et al. (2017), Neyshabur et al. (2018), & Wei & Ma. Additionally, we show that, when applied to the discriminator of GANs, it improves Inception, FID, and Neural divergence scores, while learning mappings with low empirical Lipschitz constant.