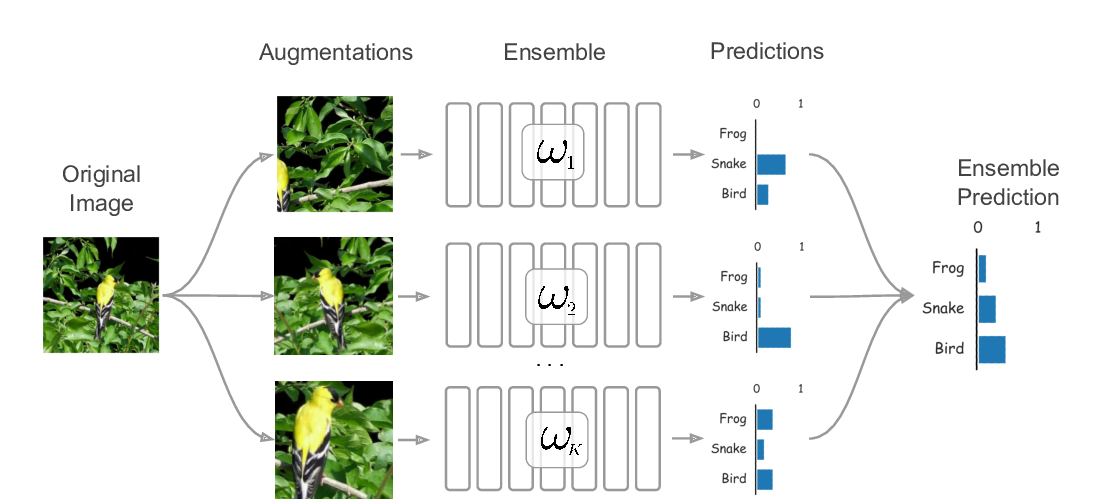
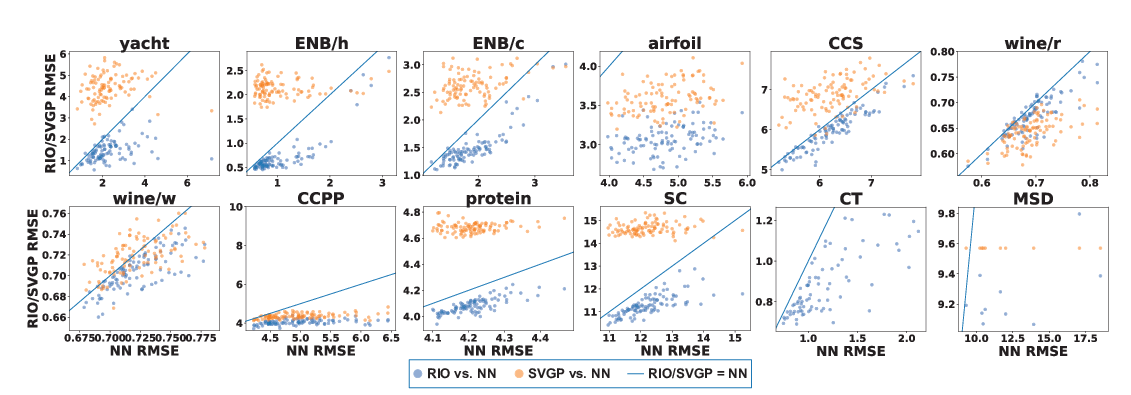
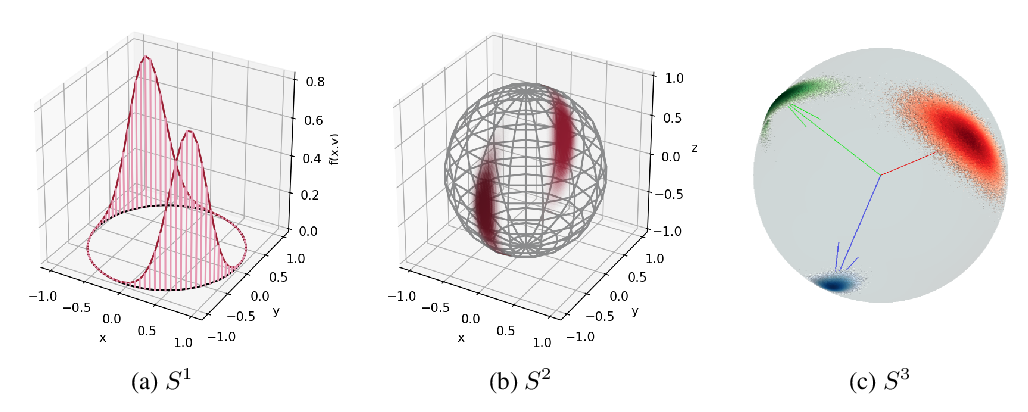
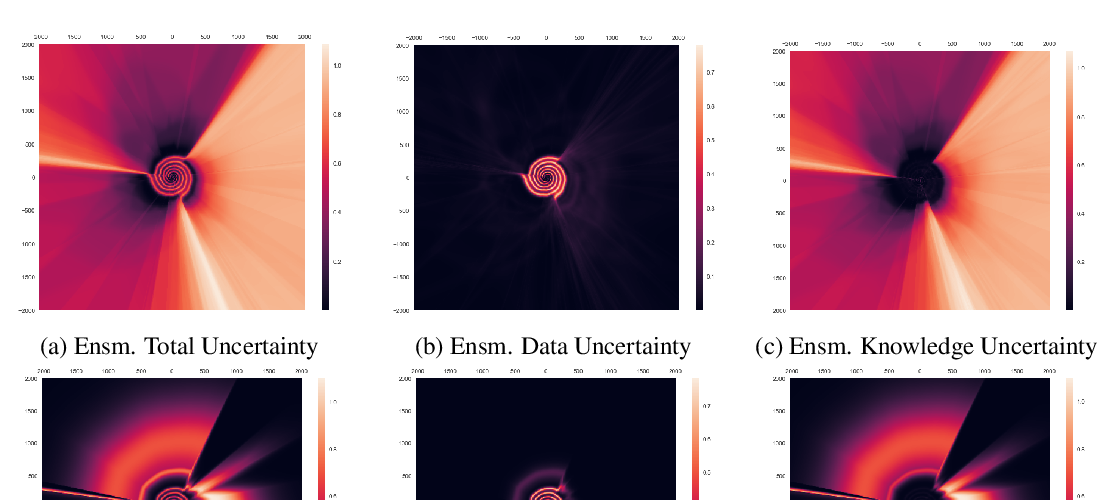
Abstract: Obtaining high-quality uncertainty estimates is essential for many applications of deep neural networks. In this paper, we theoretically justify a scheme for estimating uncertainties, based on sampling from a prior distribution. Crucially, the uncertainty estimates are shown to be conservative in the sense that they never underestimate a posterior uncertainty obtained by a hypothetical Bayesian algorithm. We also show concentration, implying that the uncertainty estimates converge to zero as we get more data. Uncertainty estimates obtained from random priors can be adapted to any deep network architecture and trained using standard supervised learning pipelines. We provide experimental evaluation of random priors on calibration and out-of-distribution detection on typical computer vision tasks, demonstrating that they outperform deep ensembles in practice.