Abstract:
We study the interplay between memorization and generalization of
overparameterized networks in the extreme case of a single training example and an identity-mapping task. We examine fully-connected and convolutional networks (FCN and CNN), both linear and nonlinear, initialized randomly and then trained to minimize the reconstruction error. The trained networks stereotypically take one of two forms: the constant function (memorization) and the identity function (generalization).
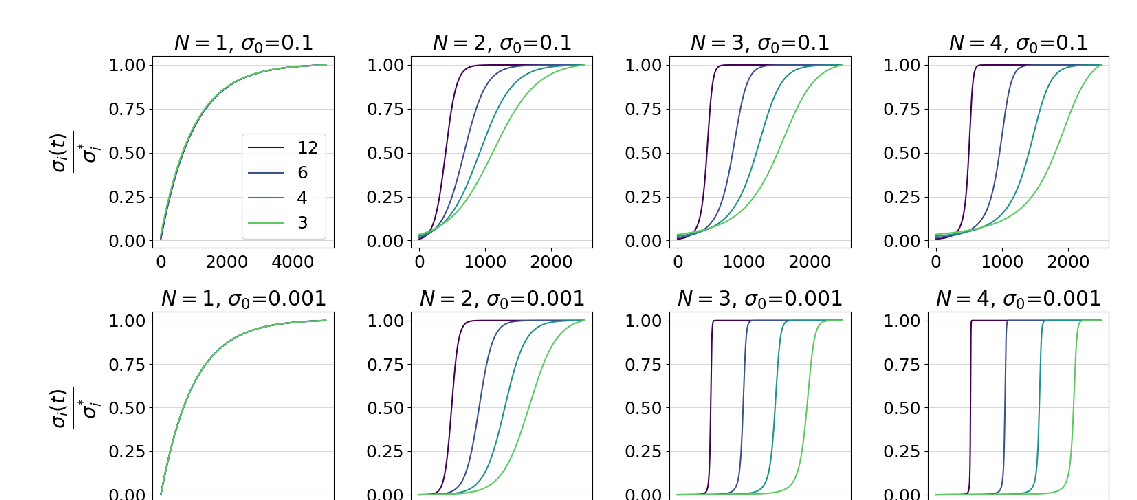
We formally characterize generalization in single-layer FCNs and CNNs.
We show empirically that different architectures exhibit strikingly different inductive biases.
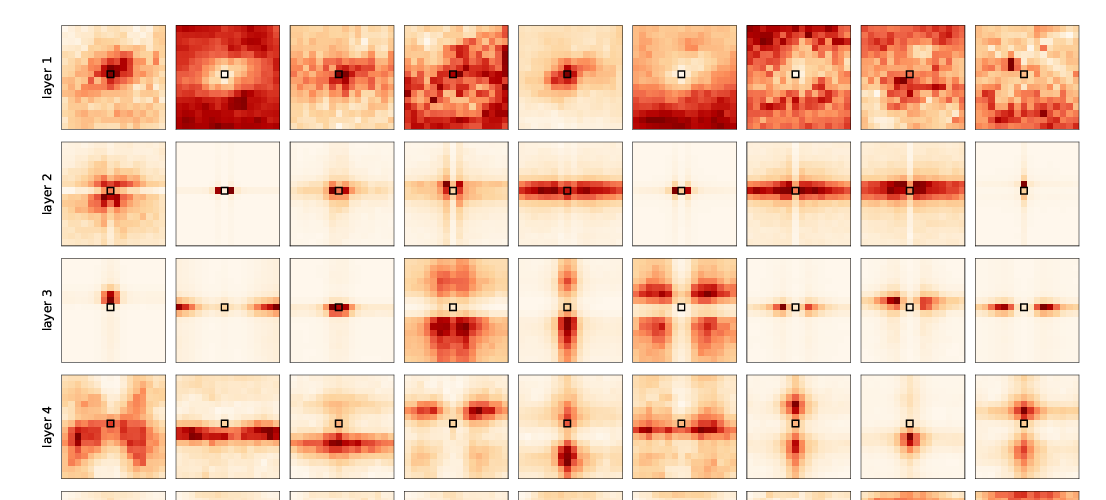
For example, CNNs of up to 10 layers are able to generalize
from a single example, whereas FCNs cannot learn the identity function reliably from 60k examples. Deeper CNNs often fail, but nonetheless do astonishing work to memorize the training output: because CNN biases are location invariant, the model must progressively grow an output pattern from the image boundaries via the coordination of many layers. Our work helps to quantify and visualize the sensitivity of inductive biases to architectural choices such as depth, kernel width, and number of channels.